[k l g j g j Cj [k l。
其中hg * c是c通过可分离滤波器hg的卷积(即先沿列通过h卷积,然后沿行通过g卷积)。在每个尺度上,我们有三个小波图像,ml,m1,a?,并且每个图像的大小与原始图像相同。因此冗余因子是3(J - 1) + 1
该过程采用与小波变换相似的滤波器组来实现,且没有降低采样性能。在图1中,给出了一个典型的未拟合小波变换滤波器组。
-
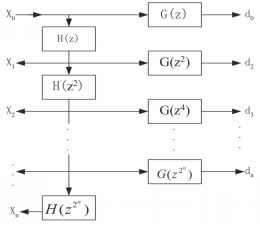
- 图1所示。未修饰小波变换的滤波器组
因此,以牺牲冗余为代价,非拟化小波分解提供了鲁棒的纹理特征。我们使用非拟合系数作为SAR图像分析的特征。
这些特征之间的简单组合通常不适合SAR图像分割,因为这样会造成冗余和计算复杂度的增加。因此,有必要找到最适合SAR图像分割的特征子集。该过程通常被认为是一个优化问题,可以使用顺序前向选择(SFS)算法。
序列正向选择是一种传统的特征选择算法。它从一个空的特征子集开始。在每次迭代中,恰好有一个特征被添加到特征子集中。为了确定要添加哪个特征,算法试试性地向候选特征子集添加一个尚未选中的特征,并测试在试试性特征子集上构建的标准函数。得到准则函数最大值的特征一定会被加入特征子集。在实验中,终止条件为最大迭代。本文以欧氏距离为准则函数,以分辨率最高的系数为首选特征。
为了避免SAR中的噪声,我们通过Kuwahara滤波器对这些选定的特征进行滤波。由于蒙版中包含的边有较大的方差,Kuwahara滤波器t7!设计如图2所示。分别计算这四个掩码的方差,然后用方差最小的掩码的特征均值来改变中心特征。实现步骤如下
•• |
J |
•• |
•分别计算四个掩码的方差。
•选择方差最小的掩码,并计算该掩码中特征的均值。
•用这个平均值改变中心特征。
•对每一个特征进行此程序。
均值漂移是由Fukunaga和Hostetler在1975年提出的,后来基本上被遗忘了,直到Dorin Comaniciu的论文[34]重新引起了人们对它的兴趣。Dorin Comaniciu证明了均值偏移过程是一种非常通用的特征空间分析工具,可以为许多视觉任务提供可靠的解决方案。它试图获得特征空间的概率密度函数的模式,使用密度函数的非参数估计。通过寻找特征空间中密度最大区域的中心,自动获得聚类数量。
为了估计密度函数,我们使用核密度估计(在模式识别文献[33]中称为Parzen窗口技术)。假设特征降维为d,点X = {X1,…,XN} cWd来自概率密度f (x)。则定义在点x处用核函数K(x)和窗口半径h求得的多元核密度估计为:
继续阅读:Hr hh hs Hr
这篇文章有用吗?
